There has been some recent blog discussion on comparing observations and climate models consistently. Here is my effort at such a comparison using the CMIP5 models which are already available.
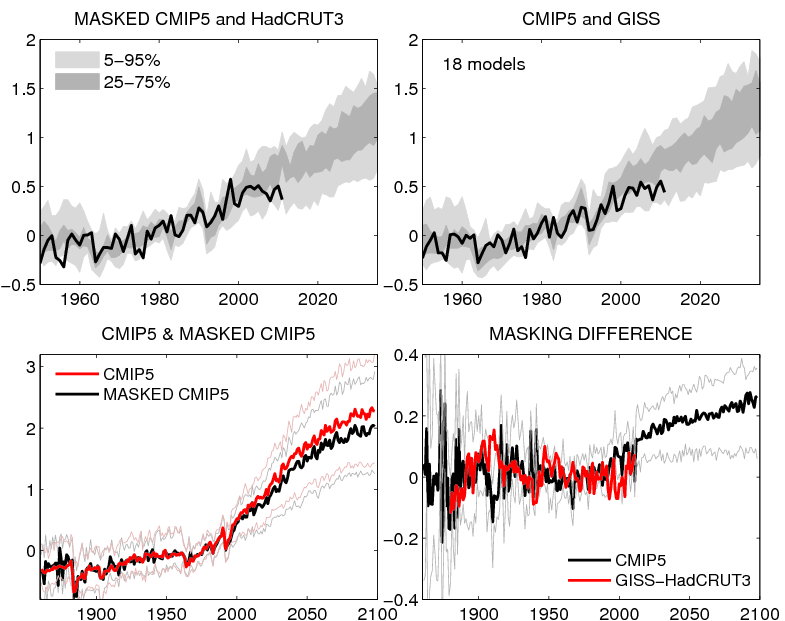
Estimating “global temperature” from observations raises lots of subtle issues about how to compare these observations with climate models. Below is (I hope) a consistent comparison for two observational datasets (HadCRUT3 and GISS). The GISS estimate extrapolates over unobserved regions of the globe (mainly the Arctic) so can be compared with the full field from the CMIP5 climate models (top right). For HadCRUT3, which only uses 5°x5° gridboxes where observations exist, the temperature trends are slightly smaller because the faster warming Arctic is not included. The CMIP5 models can be “masked” in the same way as the historical observations to produce a fairer comparison (top left).
The differences between the model estimates (bottom left) become larger into the future (assuming the same observational coverage as Dec 2011) – up to 0.2°C by mid-century (bottom right).
In summary, these comparisons need to be performed carefully, and when they are, then both observational estimates of global temperature sit in roughly the same quantiles when compared to the models in the recent period, i.e. on the lower side of the model projections.
Hi Ed
Nice post, thanks for doing it.
I think it may be worth noting the implications of your famous paper here, ie: that uncertainty in the earlier part of the projections is dominated by internal variability, not the model response (and not emissions either). Hence, just because the observations are in the lower quartile of the multi-model projections at the moment, this does not necessarily imply that most of the models are over-estimating climate sensitivity – the recent observed temperatures may well be within the range expected from internal variability as expressed by differences between the models, so the models and the observations are fairly consistent.
(Of course this doesn’t actually rule out the models being systematically wrong, or there being some external forcing that we are not accounting for, but internal variability may still provide a perfectly reasonable explanation.)
However, I guess further analysis is needed to quantify the internal variability component as distinct from the model uncertainty here as you did in your paper for CMIP3, and really systematically test whether the obs are purely within the CMIP5 internal variability range – but I guess that’s another whole paper…!
What do you think?
Cheers
Richard
Thanks Richard – yes, determining whether the recent period is due to internal variability or missing model processes is important. I hope to update the HS09 work for IPCC AR5, which may help, although the model ranges in internal variability are also huge – see here for global mean, and here for regional temperatures.
cheers,
Ed.
Am I right in thinking that the model runs date only from the last couple of years? I think it would be more useful to see how things stacked up where more time has elapsed.
When was CMIP4?
Hi Bishop,
Yes, these are the latest model runs being prepared for assessment in the IPCC AR5, and not all have been released yet. And more years will aid the comparison of course.
CMIP4 didn’t really exist – the main motivation was to sync the numbering systems between CMIPs and IPCC ARs…
cheers,
Ed.
The other reason there was no CMIP4 was because after CMIP3 there was another model intercomparsion project called C4MIP, short for CCCCMIP or Coupled Climate-Carbon Cycle Model Intercomparison Project.
This specifically looked at models that included an interactive carbon cycle (which the CMIP3 models did not – CMIP just stands for Coupled Model Intercomparison Project, and in those days, “coupled” just meant atmosphere-ocean.)
Several (but not all) of the CMIP5 models include an interactive carbon cycle, so it is the natural successor to both CMIP3 and C4MIP. The progression of similar acronyms is, however, merely a happy coincidence!
‘…observational estimates of global temperature sit in roughly the same quantiles when compared to the models in the recent period, i.e. on the lower side of the model projections.’
Am I correct in thinking that this can be expressed:
‘the models do not match observation’
or would that violate a fundamental climatological tenet of some sort?
Hi ZT,
This is a common misconception – we know there is considerable natural variability in the climate system which causes the observed trend to be larger and smaller than the projected trend at different times. The models also demonstrate this behaviour, and individually show decades which cool globally. We happen to be in a position where the recent observed trend is lower than the mean model projection, but within the possible range. So, the observations and models are still consistent. If the relatively flat trend continues for another 5-10 years then they might not be.
cheers,
Ed.
Many thanks for the response, Ed.
Do I understand correctly – you are saying that the observations have variability and the models have variability – but if the models fail to reproduce observed variability, as they apparently do, this is regarded in climatology as ‘consistent’?
I am also most interested in the derivation of the additional (5-10 year?) time frame that you mention. Can you explain the origin of this time window? (The ‘falsification’ windows, lets call it). Does it relate to a well known periodicity in the variation of the earth’s temperature versus time? [snip rest of comment]
Hi ZT,
This is another common misconception – the chaotic nature of the climate system produces periods when the observed trends are lower (and other periods are higher) than the mean model trend. The timing of these variations are (simplisticly) unpredictable, so we don’t expect the models to reproduce this timing – the models are only designed to project any trend, with the correct statistics of the variability, rather than match the temperature from year to year. E.g. the extreme warm year of 1998 due to El Nino would not be expected to be in the model projections in 1998. If it was, it would be by chance, and the model may produce such a year in 1995 or 1999 instead.
Try this article or this one.
cheers,
Ed.
Many thanks for the response, Ed.
No doubt this is a common misconception, but I don’t see a discussion in the links of the ‘falsification window’. (Did I miss it?)
Is there an article where you have run a model backwards in time and shown how the model reliably reproduces observed temperatures trends based on only input from the present? (Presumably this is an entirely straightforward and simple exercise routinely employed to demonstrate the predictive power of the models). It would be interesting to know, for example, how the GCMs account for the LIA.
Hi ZT,
The first article includes a brief mention of the fact that the maximum time between new global temperature records in the range of models used is 17 years. HadCRUT3’s peak global temperature is in 1998, although the Arctic effect above is not included in the 17 year estimate, which would increase it. There are other papers which suggest that a cooling trend of more than 15 years is not consistent with the models. So 5-10 years is a rough estimate.
The climate models are regularly run using known inputs from 1850 onwards, and increasingly from year 1000 onwards (http://pmip2.lsce.ipsl.fr/) to look at MWP and LIA – numerous papers on this too. This is not simple though, as we don’t know all of the radiative forcings which impact climate (e.g. GHGs, volcanoes, solar variability) very well back that far.
cheers,
Ed.
Hi Ed, The first paper says ‘it is possible that we could wait 17 years’ (when discussing the warmer years). This seems to be presenting a possibility – and I’m asking how the 17 was derived, logically or mathematically.
Your second point is not quite what I’m asking for. I would like to know that a model that is being used to predict the future can also predict the past, with the same assumptions. (This is the beauty of computational models, you can reverse he sign of time!). Please tell me that this basic validation is performed for the GCMs.
Hi ZT,
In the example you talk about, I took all the model simulations for the 21st century and, starting from every simulated year, looked at how many years had to elapse before a higher global temperature was reached. Much of the time it was a few years, but sometimes it took more than 15 years before a higher temperature year arrived. This was to help inform the often used discussion on how long we have to wait before 1998 is beaten as the record global temperature (according to HadCRUT3). Hope this makes sense now, but the 17 years should not be taken literally – I would put a 15-20 year range on it.
As for the reversing time question – I’m not sure it’s as simple as you suggest, and as far as I know, is not done. The climate system is extremely non-linear with critical thresholds – the direction of time is important. However, for fun we do try spinning the Earth backwards!
cheers,
Ed.
Hi Ed,
Many thanks for your reply. If from a small number of trials your model reaches some arbitrary value in 17 years does not mean that if your model reaches an arbitrary value within a 17 year period it is valid. (I’m writing 17 rather than 15-20 because I would prefer if this topic were not so fuzzy). This, I’m afraid, does not make sense.
I would be interested to know if you have considered whether your model is statistically distinguishable from a random walk. (I suspect not). I similar test should be applied to the observations (i.e. the temperatures that you are trying to reproduce).
As to reversing time – of course you can do this – as your illustration of reversing the rotation of the earth illustrates. From a given starting point, it should be quite straight forward to ‘predict’ the past, as well as the future. If you cannot predict the past, we can have no confidence in the future predictions!
As for running models backwards in time, I’d just like to point out that this is impossible, and not just for computational reasons, in fact any simple diffusion process becomes unconditionally unstable with a negative time step – a small variation in a spatial field gets more and more bumpy as time runs backwards, just you would expect from the fact that bumps smooth out in forwards time (drop some ink into a glass of water for a quick demo).
People do sometimes talk about running models backwards in the context of variational assimilation using a model/adjoint pair, but it is specifically the adjoint that has the direction of time reversed, and the diffusion operation takes that into account (says someone who built a model/adjoint pair by hand some time ago, and learnt most of it by a process of trial and error 🙂 )
Running the model backwards in time is NOT the way to verify models.It is much better to run the model in the normal way, forward in time, using the best available values for the forcings.
If we want to see accuracy of the model over a few decades, then the model should be initialized with the state of the climate system at a given point in time and the run forward. Often though, the model is spun up to a near- equilibrium state by running for a long period using a fixed set of forcings, such as for 1850AD, which is appropriate for longer term comparisons and forecasts.
Of course, this type of hindcasting is not a truly independent test since both the historical forcings and the historical observed temperatures have been changed and updated — almost always in ways that improve the model to observation comparison.
The discussion of running models backwards in time is interesting, but not relevant.
Hi Ed
Interesting little analysis – thanks for sharing.
I don’t suppose you know if anyone is compiling a list of CMIP5 papers? It would be good to know what is being done.
Ta
Andy
Thanks Andy, This helpful website is currently unhelpful!
cheers,
Ed.
Blimey, not sure I’ve got time to read all those!
Lucia regularly does this kind of comparison at her ‘Blackboard’ blog. See for example her post “More sensitivity to baselines” in December. She uses SRES projections.
Her conclusions are usually similar to yours – that the observations are close to the bottom of the model range.
She also often makes the point that it’s very easy to set up your comparison to get whatever answer you want.
McIntyre says that if you use the same method as Santer et al 2008 but use up-to-date data you get an inconsistency between models and observations. They also have a paper in atmos sci letters but it’s quite heavy on statistics.
Would it be possible for you to do a masked CMIP5 vs. Hadcrut3 SImilar to the upper left graph, but covering the 1900-1960 hind cast period? (but still keeping the common 1961-1990 baseline)
Or perhaps add HADCRUT3 to the bottom left graph.
At which year In the run did the forcings change from historical estimates to projected forcings?
When was the model run completed?
Hi Charlie,
A figure showing the spread in models from 1860 onwards is here. The observed forcings are used until 2005, when the RCP4.5 scenario takes over. These model runs were completed within the past 6 months!
cheers,
Ed.
Thanks! Now I just need to figure out the significance, if any, in the excursion of HADCRUT3 below the model lower 95% band around 1910, then going above the upper 75% line by the 1940s.
The large variation is GISS – Hadcrut3 around 1910 (1920?) hints that the model vs. observation difference might be mostly an issue withs obs.
Remember that prior to 1950 we didn’t have that great of coverage for the land-based record. The only significance of any disagreement between data and model is bias in the data prior to 1950.
If HadCRUT3 uses 5°x5° gridboxes why this:- “the global mean is calculated as the separate average of NH and SH (as done by the Met Office and CRU) to ensure that the NH doesn’t get more weight from the higher density of observations.”?
Nothing to do with the Arctic, just puzzled, if the globe is gridded and the value of a grid calculated how does the density of observations give more or less “weight”?
Very simply, because there are more gridboxes with observations in the NH than the SH, i.e. there are lots of empty gridboxes in the SH without observations in HadCRUT.
Ed.
Thanks Ed,
So how do they value the empty SH gridboxes? Or don’t they? In which case do we have another anomaly in the SH similar to the Arctic?
Hi Green Sand,
The empty boxes are unvalued. So, yes, the Arctic is the main reason for the differences as it is warming fast, but there are large areas of the Southern Ocean, Antarctica and some of Africa where the observational coverage is limited. You can see that in this figure of the most recent observations. All of the white areas are masked out in the analysis I presented above, and this is done separately for each month, as the availability of observations changes over time.
Ed.
Ed Many thanks for the replies, I am starting to get a better comprehension though not yet sure of the implications.
Whilst on this subject could you possibly help me with the following re the Arctic “issue”?
The MO page linked below carries the following:-
http://www.metoffice.gov.uk/research/climate/seasonal-to-decadal/long-range/glob-aver-annual-temp-fc
Figure 3: The difference in coverage of land surface temperature data between 1990-1999 and 2005-2010. Blue squares are common coverage. Orange squares are areas where we had data in the 90s but don’t have now and the few pale green areas are those where we have data now, but didn’t in the 90s. The largest difference is over Canada.
Could you please explain why we had the Canadian data in the 90s and not in 2005-2010? I don’t believe that any of the Canadian Arctic stations had been taken offline? If that is the case why were they excluded? If my understanding is wrong could you please point me in the right direction to find out which stations were taken off line in Canada?
I don’t make the datasets – you would have to ask CRU or the Met Office – or download the station data itself from:
http://www.metoffice.gov.uk/hadobs/crutem4/data/download.html
cheers,
Ed.
I like this bit, “The GISS estimate extrapolates over unobserved regions of the globe (mainly the Arctic) so can be compared with the full field from the CMIP5 climate models (top right). For HadCRUT3, which only uses 5°x5° gridboxes where observations exist, the temperature trends are slightly smaller because the faster warming Arctic is not included.”
GISS has to extrapolate because of the paucity of observations for the Arctic. HadCRUT3 doesn’t and gets a smaller temp trend. In other words, it seems to be that the GISS trend is running warmer because it includes made-up figures for a part of the globe for which little temp info exists. Is it the case that we only think the Arctic is warming faster because GISS smears some adjacent temps over the Arctic? There must surely be more to it than that.
Of course there is. The observations that are included from the edge of the Arctic are warming fast, the melting ice is a bit of a hint, as well as sparse temperature records which don’t make it into the reconstructions like HadCRUT, the atmospheric reanalyses… The climate models also suggest that the Arctic will warm faster than anywhere else.
cheers,
Ed.
There is a statistical justification for the extrapolation as well:
Rigor et al. (2000) have shown that surface air temperature obs from the Arctic for the period 1979-1997 are well correlated over a radius of ~1000 km for all seasons except summer (where the correlation length scale dips to 300km). I think that this justifies the GISS method.
Perhaps worth observing that it’s actually interpolation since we are talking about the surface of a sphere. And it is entirely routine and commonplace in all sorts of geophysical data analysis (and probably elsewhere, but my knowledge is more limited).
Boo, it’s the terminology police! But you’re right (and I even “corrected” myself from interpolation to extrapolation after re-reading the comment above).
Bruce, in fact it’s even worse than this, because the GISS stations near the arctic are warmed by artificial adjustments (in fact, past temperatures are adjusted downwards). See several recent posts at Paul Homewood’s blog notalotofpeopleknowthat. This fabricated warming is then amplified by the GISS extrapolation.
I’ve not seen Paul’s blog before but is this “fabrication” similar to one that Lindzen had to apologise for presenting recently?
I followed your link, Andy. It’s good to see that both Lindzen and Hayden were gracious enough to provide open apologies for what was Hayden’s accidental mistake. You have used two scientists’ gracious integrity to shoot down a totally different point. Well done. The way that the Arctic extrapolation is done is worthy of investigation. The integrity of the few temperature stations in that area is paramount. I have seen photos to suggest that their siting is far from ideal. A busy airport, where white snow is regularly cleared to reveal black bitumen, is not the ideal site for an Arctic temperature station.
I think it was a legitimate question: is there any similarity between the non-fabrication that Lindzen was talking about and this other reported fabrication. I had a quick look at Paul’s blog and didn’t see anything about GISS. Without any links to the specific posts it seems like an important point to clarify.
The various methods of infilling and extrapolation/interpolation are interesting, but this blogpost sidesteps those issues by masking the model output and only comparing model to observations where and when they coincide (well, at least coincide to the resolution of a 5×5 degree grid).
@Green Sand — I believe the problem is that there are more empty grid boxes in the SH than in the NH. This means that there is a slightly different result from averaging all non-empty grid boxes globally vs averaging for each hemisphere and then taking the average of the two hemispheres.
Since the SH shows less warming, the average of NH + SH has a slightly lower trend than a global average with many missing SH grid boxes. Kind of the opposite problem that Hadcrut3 has vs. GISS because of missing arctic grid boxes.
Hi James,
Thank you for your comment on reversing time!
Could you explain mathematically why time cannot be reversed in GCM models? I would have thought that an iterative model which takes you from step-n to step-n+1, would surely be reversible. Or are you saying that the end points of GCM models are as random as plumes of ink mixing in water? (and therefore not worth reversing).
I did not understand your second paragraph – at all!
http://www.flow3d.com/cfd-101/cfd-101-computational-stability-heuristic.html
(which I found with a few seconds googling, BTW)
ZT I suspect you don’t really want the mathematical answer (which is that du/dt = – del^2 u is ill-posed). The physical reason is like your example of mixing ink in water, it’s not a reversible process – once the ink is well mixed you could never figure out where it had originated from.
Hi James,
The link you found so rapidly makes no mention of changing the sign of time.
A question for the climate modeling elite: When the medical examiner tells the detective that ‘the time of death was between 1 and 2 am’, how did he or she arrive at that conclusion? Did he or she waffle about mixing ink, or did he or she effectively allow time to be reversed until the temperature of the body [sic] in question became 98.6F (or 37C)?
Many things are not reversible in theory and many more are not reversible in practice. A week after death the time of death could be theoretically determined from the temperature but in practice we don’t have accurate enough info to accurately hindcast when the body temp was 37C.
The “waffling” about ink drops is a simple example. The diffusion of a drop of ink into a glass of water can be modeled fairly accurately. It is much more difficult to start with a nearly uniform mixture of ink and water and run the model in reverse to determine where in the glass the original drop started from.
There are many cases where multiple starting points lead to the same result. A model running backwards won’t be able to determine which of the infinite possible starting conditions is the correct one.
I mention the forensic analysis of temperatures to illustrate that it is routine to model temperature in the past based on measurements in the present. (In fields other than climatology). This example is well known to anyone who watches TV detectives.
I remain baffled by your trying to invoke ink-mixing as a reason from not properly testing your models. You have a non-equilibrium fluid dynamics situation (the present climate), you want to predict a future non-equilibrium fluid dynamics situation (the future climate). Please explain why you cannot predict a past non-equilibrium fluid dynamics situation (the past climate) from present conditions.
This would seem a fairly basic test to me. Typically in science models are used to explain what is already observed from well defined assumptions before they are employed to predict the future. Perhaps this is just ‘not done’ in climatology – but I do not see why it cannot be done.
I would have hoped it was sufficiently obvious as to not need stating that reversing the direction of time in a diffusion equation is mathematically equivalent to reversing the sign of the diffusion coefficient.
If that makes me part of the “climate modelling elite”, then so be it. But it’s something I encountered some years before I got involved in climate modelling.
Hi James,
If I google ‘”negative time step” in diffusion model’, I see 3.6 million hits, this is the first hit, and it appears to be doing reverse CFD. Is this paper incorrect, or simply misguided?
https://engineering.purdue.edu/~yanchen/paper/2007-7.pdf
(then please review hit 3,599,999 etc.)
ZT Sorry to butt in.
Your forensic analysis of body temperature analogy and James’s drop of ink analogy are actually remarkably similar.
If we were to catch James’s ink drop very quickly after it hits the water then it may be possible, from the dispersion pattern, to determine where it made first point of contact with the water. But after a certain period of time the ink will become so well mixed in the water that this is nigh on impossible.
Likewise, if we were to take a rectal thermometer reading, and use the Glaister equation to determine the time of death of a body, a fairly accurate estimate could be made within the first 24 hours. But after the heat has dispersed into its surroundings, and the body reaches the ambient temperature, then similarly the heat has become so well “mixed” in the body/atmosphere that it is nigh on impossible to differentiate between the two.
“Typically in science models are used to explain what is already observed from well defined assumptions before they are employed to predict the future.” – Yes, by the use of hindcasts or in certain spatial/time-frame restricted scenarios. For example the paper you refer to above is just such a scenario. It conducted inverse CFD modelling of contaminant transport in a small office 32 seconds after release.
Also. Apart from the dispersion problem, and I am guessing here, would not taking a complex model and then attempting to reverse the time direction involve changing the maths. i.e. making a different model! The paper you cite involves the development of a new quasi-reversibility equation for their inverse model. i.e. different maths/a different model than would be used for standard computational fluid dynamics.
I’m sure I could have said all that in a more succinct way. I am also a complete amateur so all corrections are welcome.
I am not the one to be discussing details of climate models, having never written one myself. But I have written (and published on) specialized applications of CFD and can say something about ZTs comments here.
If we run CFD equations “backwards” this system can yield instability, because viscous losses run forward yield what looks like energy sources which run backwards. … and energy sources is what you need to have in order to drive self-sustained oscillations and even exponentially growing solutions (which can happen here, since if the losses are proportional to amplitude or velocity when moving forward in time, then the amount of extra energy injected into the system will grow as the amplitude and velocity grow too when it is run backwards).
It turns out that small measurement errors get amplified, and these errors grow and you still end up with instabilities if you wait a long enough of a period of time.
So the short answer is there is a time scale over which “it doesn’t matter” if you run the system backwards, but as long as there are finite losses (when run forward) eventually the system will become unstable when run in reverse.
We “know” all this when we write CFD solvers. Even for strictly spatial solvers, there are “right ways” and “wrong ways” to solve the equations (some solution methods that would work in the absence of numerical error blow up on you in practice).
I am asking for some validation or testing that is all. Apparently running the simulation in reverse is difficult (though not impossible for some of the CFD world – and that was just the first hit of the 3.6m returned by Google).
So how does the climate modeling world test models? I heard Julia Slingo say to parliament that GCM models are tested every day – during routine weather forecasting. Is that the state of the art?
Are there examples of predictions made by the GCMs which do not closely follow their input data, and therefore provide insights into observed phenomena like the LIA or MWP? Please cite these examples.
I am sure that you are constantly asked for illustrations of successful predictions – surely this cannot be that difficult?
@ZT
hindcasts!
Regarding ‘hindcasts’, when I read:
‘The simulations above (‘projections’) are initialised by simulating the climate with constant 1850 forcings for a few hundred years to get the model into equilibrium, before using observed forcings for GHGs, solar, aerosols etc, from 1850 to 2005, and then a scenario of future forcings to 2100.’
…and…
‘Of course, this type of hindcasting is not a truly independent test since both the historical forcings and the historical observed temperatures have been changed and updated — almost always in ways that improve the model to observation comparison.’
I don’t get the sense that the models are predictive in any scientific sense. My suspicion is that the models give back to you what you put into them “then a scenario of future forcings”, with some noise (and even that noise does not match the observed “noise”).
That is my hypothesis – please disprove it.
Please list the predictions which do not match the inherent input ‘forcings’ which have been made with GCM models.
Hi ZT,
The Met Office shows its forecasts for the following year here in Fig. 1:
http://www.metoffice.gov.uk/research/climate/seasonal-to-decadal/long-range/glob-aver-annual-temp-fc
They started the forecasts in 2000, and have a pretty good record.
You are entitled to your beliefs about the models, but please take on board what people are telling you here.
cheers,
Ed.
What? All predictive models, in whatever field of science, “give back to you” a prediction based on “what you put into them”.
I am interested to know what other constraints you would give the model other than “a scenario of future forcings”?
Err no – models (if the have any value) allow you to deduce something relevant about the system. If the model assumes steadily increasing heat (because of projected ”forcings”) and running the model give you steadily increasing temperatures – you haven’t learnt much of anything (in my opinion).
If your model lets you discriminate between the various possible causes of the Little Ice Age, or the MWP, then you have something interesting and validated.
Of which type are the GCMs?
Basic physics tells us that, for instance, adding more CO2 to the atmosphere is going to warm things up.
Constructing a climate model that includes all the known forcings and feedbacks could maybe tell us by HOW MUCH it will warm up?
This could be interpreted as learning something interesting about the system.
Regarding many of the other points you make, I find your logic a little difficult to make sense of. You also seem to blithely ignore much of the information other people have posted here.
[snip – please keep on topic, and avoid insuations about people’s conduct.]
Strange that you should snip my comment – I was simply continuing the time of death estimate analogy that has been previous discussed on this thread.
Ed
I’ve got a real problem with just how fat the grey area is getting.
Ignoring the future can you explain to me why the grey area is getting wider as we move thru the graph. I’m just eyeballing this but much of the 1970’s, 1980’s and 1990’s the grey area looks to be about 0.3oC wide while 2000-2010 it’s maybe 0.6oC or more. That seems like a huge rise in a time when I would think some of the uncertainties should be reducing due to our better monitoring and understanding of the system. Shuoldn’t we be narrowing many of the parameters and so therefore the models be following more closely each other. Shouldn’t the grey be getting narrower at least up to the present day?
Hi HR,
Thanks – this effect is partly due to the standard 1961-1990 reference period used. But we would not expect the grey area to narrow more recently anyway, as the parameters governing the physical processes in the models are fixed through time.
Ed.
Thanks Ed for the reply, sorry for taking up more of your time but I’d like to understand this more clearly.
The link you post in reply to Dead Dog Bounce below clearly shows what you are talking about. The grey area is noticeably tighter between 1960-1990 then all the other periods. You state earlier that these model runs include forcing data upto 2005 and also that the physics behind these processes aren’t changing. So it looks to me like the tight grey from 1960-1990 followed by the widening of the range upto 2005 is some sort of methodological artifact. Presumably if you make the baseline 1960-2005 in these model runs then the grey area would tighten up for the period 1990-2005.
This article seems to rest on the fact that the obs temp are still within the grey area of the ensemble range, so we have to understand what the grey area represents. It doesn’t seem to represent internal variability of the climate system. That would mean internal variablity was constrained within a narrow band from 1960-1990 and then underwent some sort of breakout afterward. So if the grey area is an artifact of the method then I don’t see any reason to take reassurance from the fact that the obs are still within it.
Yes, the choice of reference period does make small differences. But, if you use a 1880-1909 reference period instead of 1961-1990 to be as far away from present as possible, the conclusions don’t change: see here
cheers,
Ed.
Can you run the comparison between Hadcrut3 and the models, with a starting year of 1940?
A figure showing the spread in models from 1860 onwards is here.
I’ve looked at the variability in climate, assumed homoscedasticity, and used the averaged temperature power-spectral density from 1900-2010 to generate Monte Carlo estimates temperature that include natural variability, by inverse-Fourier-transforming the Fourier amplitudes together with a random phase model.
Here is a figure of my simulation results. One of these is real climate (detrended) the other is an instance of my Monte Carlo simulation. My model output (the bottom) misses the peakiness of El Niño events such as the one in 2007, but otherwise is fairly reasonable in its representation of climate variability.
Anyway, I compared this model to Lucia’s econometrics based approach (relevant link) in this figure, which shows my estimate of effect of natural fluctuations on OLS trend, and shows the 1-sigma uncertainties as a function of time (double them to get the 95% uncertainty bounds of course). Lucia’s estimates are also plotted on that figure.
I bring this up because of ZTs questions about where the number comes from for how long you’d have to observe climate before you could distinguish a given difference in temperature trend. Let’s suppose for example that the data are giving a 0°C/century warming since 2002, and the models are giving a 2°C/century warming. Let’s also assume that the models exactly reproduce the statistics of the natural variability.
When computing difference in trends, the uncertainty in the difference in trends, is given by sqrt(2) * sigma_T. The 95 percentile of that is 2 sqrt(2) sigma_T, equating the two gives you need sigma_T < 2/(2 sqrt(2)) = 0.7°C/century. That suggests you need 15 years to separate even a relatively large difference in trend at the 95% CL.
And then the question is “what have you learned?” It seems to me it either means the physics of the models is incomplete or the assumed forcings are wrong, or both.
There is a recent paper by Shindell and Faluvegi that suggests that the main difference between models and data could be accounted for by uncertainty in model forcings, namely increased industrialization of China and India may be producing a greater aerosol cooling than is assumed in the model aerosol forcings.
So even failure to agree between model and data doesn’t necessary paint a simple picture for people.
Mr. Hawkins,
When you perform a model run or ensemble of runs and you say “The observed forcings are used until 2005”, how is the observed temperature initialized or tracked in the models? Is observed temperature data used by the model from year xxxx – 2005?
It seems to me that what would be needed to validate a model would be to use the observed temperature up to the year 1990 for example, and then use the most up to date observed forcing data for solar, aerosols, volcanoes etc. With an initial temperature input and up to date forcing inputs, how well does the model fit the temperature observations to date. And this might also satisfy those asking for a model to be validated through a hindcast.
Whatever you are actually trying to forecast with your model, needs to be frozen in time. And I’d think that freezing the model input at 2005 tells us very little about how it is performing. Why not initialize it with observed temp from 1990 but use up to date forcing inputs and see how well the model output matches observed temperatures to date? Is that kind of analysis ever performed?
Thanks.
Yes, that type of initialised forecast analysis is performed, but is technically more difficult than you might imagine – the first paper was in 2007 by the Met Office team: http://www.sciencemag.org/content/317/5839/796.short
However, if we are only interested in the long-term trend then there is no need to initialise from the observations. The simulations above (‘projections’) are initialised by simulating the climate with constant 1850 forcings for a few hundred years to get the model into equilibrium, before using observed forcings for GHGs, solar, aerosols etc, from 1850 to 2005, and then a scenario of future forcings to 2100. The fact that the models then track the observed trend well, without using any additional observations, is quite a powerful demonstration of their ability. See the longer term version of the figure here.
cheers,
Ed.
Wow! Lot of comment resulting from essentially one graph.
If internal variability is such a large thing, then I take it that if the model had been initiated in, say, 1960, then the run-up to 2012 would have been a large band – like the forecast to 2100 from 2012, but LOWER, in order for the actual events to follow the centre, highest probability area. Which would mean that the models would have suggested that, from 1960 to 2000 there might have been ZERO warming.
Would that be right? The model’s uncertainty going forward would be the same if the start date had been 1960 and none of the last 52 years of observations had been made?
Seems very strange that for something so settled and certain that the range of outcome even over the next 20 years is so large, and that being at the bottom of the range right now isn’t worrisome to the modellers.
To get back on-track with the modelling accuracy of 1960 – 2000, the global temps have to rise to about 0.75C at the end of 2015 on a smoothed basis. That’s a rise of about 0.30C in the next 2 3/4 years. Which will include at least one more drop period.
I can’t see getting back into the central swing by then. But extending the time-period out, to 2020 say, means more of a climb (to about 0.85C). The need for correction gets worse.
[snip – keep to the science]
Do the models’ natural variability assumptions include long-term, 0.3C jumps in the smoothed global temp over 3 year periods? Or short-term, non-stabilized 0.6C jumps in 3 years (so that a smoothed average could be 0.3C)?
Hi Doug,
The next few years are indeed going to be interesting! A quick glance at the historical observations clearly shows periods where you get sharp jumps in temeprature of the magnitude you mention.
cheers,
Ed.
Yep.
“Step function” changes abound, especially in the sea temperature. The lower stratospheric temperature (TLS graph), which is only weakly coupled to the surface, also seems to follow this pattern (though remember the tendency is for cooling in that region).
Note that the big step functions are “kicks” to the system from El Chinchon in 1982 (17°N) and Pinatubo (15°N) in 1991. (I’ll let somebody else explain the significance of their latitude, or you (Doug) can figure it out with a few minutes of googling).
So with the stratosphere, it appears we have a system with multiple “semi-stable states” and corrections from that semi-stable state to a “more optimal” temperature only happen after a big kick to the system.
I’ll just observe that I think it’s pretty interesting that the stratospheric temperature increases—in a manner expected by the model—after a volcanic eruption, then you see a sharp drop that descends through the previous “stable” temperature to a new lower value.
(Which does leave open the question as to what the model TLS temperature looks like in a scenario with a monotonically increasing radiative forcing… I don’t think I’ve ever looked at that.)
ZT, you entered this thread asserting that it was entirely straightforward and simple to run models backwards in time. The paper you cite quite clearly states that in fact this makes the system unstable, as I said. The paper presents some fudges to make it approximately work for their rather simple system (pure tracer advection/diffusion, nothing remotely approaching the complexity of cloud physics) under limited circumstances. So what. Directly running models backwards is not typically how inverse problems are solved in any case. If you want to try it with a GCM, code is freely available for some of them. IMO it would be a stupid idea, but what do I know, I’ve only worked on this subject over roughly 20 years, and I’m now involved in climate modelling, so must be a moron, or dishonest, or probably both. Right?
BTW if you are genuinely interested in true predictive valuation of climate models, see:
http://www.jamstec.go.jp/frsgc/research/d3/jules/2010%20Hargreaves%20WIREs%20Clim%20Chang.pdf
not forgetting
http://www.jamstec.go.jp/frsgc/research/d3/jules/2011%20Hargreaves%20Clim.%20Past.pdf
But somehow I get the impression you are more interested in argumentation than actually learning. Your choice.
Hi James,
I simply entered the thread asking for validation of some sort – I suggested a method – I pointed out the first link when googling relevant terms – there are several million more. Here is a paper employing precisely this method (running time backwards):
http://journals.ametsoc.org/doi/pdf/10.1175/1520-0493(1997)125%3C2479%3ASOFETI%3E2.0.CO%3B2
From the ‘American Meteorological Society’, by the way.
(This is essentially the second link in the list from google – we have a few million more to go). I freely admit to not being an expert in this field. However, your assertion that it is impossible to run CFD models backwards is apparently false. It is necessary to work a little harder than I realized – which I did not know – but do now!
Anyway, what I am interested in is validation – can you let me know how you validate your models. Apparently ‘running simulations backwards’ is used by some people in the CFD field – but not climatologists. What do climatologists do to validate models?
I really appreciate the patient, objective responses to most of the questions and comments on this thread. This is notably absent on most blogs. FYI, I am a research scientist in a biomedical field with more than 100 publications and more than 20 years of continuous grant funding, and I have even done some quantitative modeling of biological systems. In casual conversations with my colleagues. I have found concern that the more vocal climate scientists seem determined to defend things like “hide the decline” as well as many other unseemly (at the very least) statements in the climategate emails and Gleick’s ethical lapse. It seems that they are afraid to concede anything. This has probably created more skeptics than any of the detailed scientific arguments. I am in no position to determine if the arguments have merit (although some seem quite reasonable to me), but I know for certain that the response to criticism exhibited by vocal climate scientists is not what I would expect from researchers who were confident of their results. I would also expect occasional admissions that there was misbehavior and that some of the prominent symbols of CAGW (e.g., hockey stick) had some problems. Support for a paper that uses the output from one model fed into a second model and output from the second fed into a third to conclude that warming will cause mass migration from Mexico is also baffling. I can’t imagine even trying such a thing as this for fun, let alone consider that it would be taken seriously by peer reviewers in epidemiology. It is not clear how such things can be published in climate science.
Is my impression of climate scientists unduly influenced by a few vocal individuals who are not representative of the majority of the community, or are you guys really perfect (as at least some seem to believe)!?
Hmm – I looked at the Hargreaves reference above. This says ‘…there is no direct way of assessing the predictive skill of today’s climate models’
Hargreaves defines ‘skill’ as the predictive ability of the model beyond a linear extrapolation of the current trend.
So, from the reference that James cited, I learn that it is considered impossible to validate a GCM model in terms of its ability to make predictions. You could produce a model using a piece of graph paper, a ruler and a dice, and it would be impossible to distinguish such a model from a GCM model. (Assuming the Hargreaves paper is correct).
In a way what you are saying is right—models depend on knowing future forcings, but since you don’t know the future forcings: Some of them like solar and volcanic are unknowable based on currently understood science, future aerosol and CO2 emission histories similarly depend on future political, social and economic conditions… again unknowable.
You’d have as much luck writing a truly predictive climate model as you would a model of future change in the stock market.
So you can’t verify GCMs using validation via prediction.
This is now a test for you, ZT. If you were studying climate models, what types of validation studies would you suggest performing?
Keep in mind this is an observational science, and validation is possible in observational sciences just as in empirical, you just can’t do it in as straightforward of a fashion.
(To put it in a different arena, how do cosmological models get validated, or can they ever be validated?)
In no particular order:
1) Cosmological models aren’t being used to justify turning the world upside down – I presume that scientists somewhere are testing what they say against observation – if not – they are wasting their time (too).
2) I would test climate models by showing that they can predict something that was not fed into them. Apparently the GCM industry has decided to make life easier for itself by defining ‘testing’ out of its activities. (Nice move guys!)
3) What on earth is an ‘observational science’? Is that one where predictions are impossible and funding infinite?
4) There is some kind of denial going on among GCM people. I asked about validation/verification/testing on this thread. I provided a suggestion for how to do this – which apparently is employed in the CFD world. What I get back as a respons from the GCM world (which does at least respond – which is praiseworthy) is:
a) being told things that aren’t correct – e.g. negative time steps are an impossibility
b) a lot of bafflegab – why does this world create such strange jargon?
c) pointed to references which apparently confirm that GCMs cannot be tested via their predictions (there seems to be some sort of hope that an interested inquirer can be put off by being fobbed of by baffling references – in profuse and odd jargon)
Finally, I would like to submit ZT’s graph paper, ruler, and dice model to the journal of whatever it is that you submit these models to. Presumably it is irrefutably as predictive (sorry skillful) as any other GCM. I may elaborate it in the future to use an etch-a-sketch as the plotting medium, with an adjusted x-axis knob which prevents time reversal, by which time this model will probably be the de-facto standard employed by the IPCC.
ZT, sorry you lost me on “Cosmological models aren’t being used to justify turning the world upside down” and “What on earth is an ‘observational science”.
I’ve no patience for ad hominems nor for unadulterated ignorance.
Bye
Mangled though the meaning is probably obvious… rewrite: “So you can’t verify GCMs using validation via prediction” as “So you can’t validate GCMs using prediction.”
I’m using verification and validation in the senses used here:
Verification: was the product built right?
(E.g., does the GCM solve the set of physical equations correctly given a forcing history?)
Validation: was the right product built?
(E.g., do the physical equations and underlying assumptions and the forcing history adequately represent what is physically happening?)
I think people often confuse the two, even when they are trying to disambiguate them (I did so in my comment too).
(We can get into a meta-discussion over what “prediction” is versus “forecasting”. I think ZT is getting hung-up on the inability of climate models to accurately forecast future temperature.)
There is no accurate complete solution for fluid mechanic problems such as unsteady 3-D turbulent flows at high Reynold’s numbers, even with well posed initial and boundary conditions, and actual data (wind tunnel or flight) is always used to fill the gap (calibrate the model approximations). This allows for some interpolation, but not extrapolation beyond a short time period. Atmospheric flows are much more complicated that these flows, with phase change, unknown exact boundary conditions, and some of the physics not even known (e.g., cloud feedback and formation details). The nonlinear PDE’s and plugs (for clouds, aerosols, and poorly known long term ocean currents, for a start) for weather and climate calculations do not have sufficient spatial or temporal resolution to correctly address viscous or other dissipative processes. Simplified statistical models are used to fill the gap. Going forward or backward has the same problem. You quickly go from approximately calculating the trend, to losing all contact with where it is going. Exactly the same stability and resolution limitations hold both ways. The net result is that weather forecasts never can do well beyond a few days, and probably never will, although the number of days may slightly increase. The mistake that climate is basically different is misplaced. It is true that there are gross drivers line day and night, and seasons, and basic limitations in limits due to basic balance of energy, but there is no argument that has been made that has falsifiable support that shows that the climate can be reasonably calculated, even in average, several decades ahead. NONE. ZT is probably correct that the reversal of time should do about as well as forward calculations, i.e, GIGO.
Leonard, there is a relationship between spatial scale size and frequency content. You don’t seem to be aware of this when you are arguing they need to include weather in order to model climate. It’s true they use parametric models (others who know more of these details can discuss this if they see fit), but there isn’t necessarily a problem with this.
If you want a similar example, how about modeling meso-scale weather since you brought that up? They fail to fully model the surface boundary layer in mesoscale weather models, yet they meet with good success there. How does that gel with the worldview you’re arguing here?
An even more apropos example is the highly successful modeling surface boundary layer in large scale eddy simulations. Here you resort to the use of a sub-grid scale models to incorporate the physics at smaller spatial (and short temporal) scales.
There are even hybrid models such as WRF that nest increasingly finer resolution models inside of coarser grained ones. Also works very well.
Since it isn’t necessarily catastrophic (highly successful is neither catastrophic nor does it qualify as GIGO), I think you need to be able to write down explicit rules that tell us when it is and isn’t OK to approximate sub-grid scale physics… in other words how one goes about validating that the assumptions made in doing so. And then demonstrate that poor fools that study climate models have failed to do so.
Till then, what we have from you is at best an under-educated opinion and just one cut above ZT’s spiels.
Regarding running a model backwards, I have no clue what you were driving towards, but here’s a simple model:
x”(t) + x'(t) + x(t) = f(t),
f(t) = 0, t < 0,
f(t) = cos(t), t≥ 0,
with x(0) = x'(0) = 0.
The solution for t >> 0 is x(t) = sin(t) as you can easily demonstrate by substitute.
Try numerically integrating this backwards and see what happens. (The forwards direction is stable and well behaved of course.)
The result is quite a bit worse than just GIGO. I’m pretty sure even the poor simpletons who model climate would know there was a problem when their solutions went to ±infinity.
I agree that you cannot recover a starting point from an equilibrium situation by reversing time.
But you also can run CFD and even weather simulations backward in time – because the friction terms are not all that significant, in many instances. See:
https://engineering.purdue.edu/~yanchen/paper/2007-7.pdf
and
http://journals.ametsoc.org/doi/pdf/10.1175/1520-0493(1997)125%3C2479%3ASOFETI%3E2.0.CO%3B2
So – it is not impossible to run CFD backward – but perhaps it is not as numerically stable as one would need to ‘validate’ a GCM model.
That still leaves the problem that GCMs are apparently impossible to validate – that seems to be the position of the GCM world (right?). All that can be addressed in the GCM world is reduced uncertainty. However, this ‘uncertainty’ is measured around the supplied ‘forcings’ which completely determine the long term behavior of the model. Have I understood this correctly?
I believe we’re going in circles here—we’ve agreed you can run a model backwards in time, however the amount of time that you can do it before it becomes unstable depends on how large the losses are in the system when run forward, that governs how long the system will remain stable when run in reverse. This is not very long in a climate system (I’m not sure exactly long, but a SWAG would give days not years.)
In problems where you are interested in the source of a contaminant (for example) or the source of a signal (e.g., tomography where you’re trying obtain a 3-d map of reflection strength) you can modify the physics to stabilize time-reversed solutions. This is done e.g. by neglecting the losses in the time-reversed equations (signal attenuation losses in tomography), and is a consistent approach for solving for the point of origin, if the attenuation does not affect the forward-time propagation direction (e.g., refractory effects associated with the attenuation can be neglected in the case of tomography).
You can get to the same result by not modifying the physics, using a Monte Carlo based approach (for example), to generate a series of initial “starting conditions” and run the model forward in time, selecting the set of initial starting conditions which (within measurement error) are consistent with your outcome as the “solution” to your inverse problem.
In CFD, it is very expensive to run models forward, so the preference is to look for short cuts to reduce the computational time. In other words, the tricks used here has nothing to do with model validation whatsoever, it’s jut a method for efficient inverse solution to the problem of source localization.
As to validation of GCMs, I’d suggest spending a bit of time thinking and allowing yourself to learn something new—in this case, start with the question of what an observational science is and how one validates it (you have proven by now you can google, [snip]).
If you are really interested in the problem and as clever as you claim to be, I really think you can work out your own answers from there.
Carrick I might have you wrong but to paraphrase it seems that your replies to these critics is “If you want validation then do it yourself”
It would be an interesting situation if pharmaceutical companies could make the argument to regulatory bodies or patients that if they want their drugs validated they can go do it themselves.
Sorry to go back to basics, but surely there is only one reason to compare observations to a model and that’s to test a hypothesis.
A model is just an embodiment of a hypothesis (or set thereof). You determine the level of significance at which the null (contrary) hypothesis is rejected by comparing the predictions of the model with measurements.
If you then have a model sufficiently valid (“statistically significant”) then you can be brave and use it to predict values of the dependent variables (eg temperature) against values of the independent variables (eg time, CO2 conc, etc) that are outside the ranges in the test of significance. Of course, the model might not work there, but I’ve never heard of a better approach!
That’s what my PhD supervised drummed into my head, anyway….
SupervisOR not supervisED of course…
Ed – Isn’t this a bit flippant?
“the melting ice is a bit of a hint, as well as sparse temperature records which don’t make it into the reconstructions like HadCRUT, the atmospheric reanalyses…”
What is most happening in the Artic, is not primarily temp dependant (in short term), but driven by wind direction, ocean currents..
Should wind direction change for a few years?
ie from the BBC:
“Arctic sea ice has staged a strong recovery in the last few weeks, reaching levels not far from normal for this time of the year. Interestingly Antarctica sea ice extent is currently slightly above average, as it has been for some time.”
The much publicised 2007 minimum Arctic ice level was in large part due to the prevailing wind, which blew more ice into the Atlantic – as opposed to anything directly linked to global temperatures, as widely reported in the media at the time.
In fact The Met Office issued a press release to that end, saying the loss of sea ice that year had been wrongly attributed to global warming.
Arctic weather systems are highly variable and prevailing winds can enhance, or oppose, the flow of ice into the Atlantic. Indeed the increase in ice extent this month has coincided with a change in wind direction which seems to have spread out ice cover.
It’s too early to say whether this recovery will translate into higher levels of spring and summer Arctic ice compared with recent years, but scientists will be watching data closely in the coming days and weeks.”
http://www.bbc.co.uk/blogs/paulhudson/2012/03/recovery-in-arctic-sea-ice-con.shtml
Ed
You may not be aware that one of the reason sound outside the climate community don’t take consider statements like “There are other papers which suggest that a cooling trend of more than 15 years is not consistent with the models.” as demonstrating much of anything is the argument in Easterling and Wehrner (and implicitly in your blog post) bases that sort of claim on the assumption that the spread of weather across models with different mean response represents something about the variaiblity of earth weather. (Worse– some of their argument conflates variability that arises because some models include volcanic forcings and others don’t with internal variability we would expect during periods without eruptions from Pinatubo.)
It is quite easy to that your grey bands are not estimates of “internal variabilility” in AR 4 models so by creating colored graphs like this: [Fixed links]
http://rankexploits.com/musings/wp-content/uploads/2011/05/WeatherNoiseInModels.png
http://rankexploits.com/musings/wp-content/uploads/2011/05/ModelTraces.png
This is discussed in here.
Richard:
“internal variability”.
If you want to convince me and the sorts of readers who read my blog that the temperature spread is within the range expected of internal variability you are going to have to do some work to explain what level of internal variability is “expected”. If the answer is that “internal variability” can be estimated by taking the spread of variability from a collection of models with different mean responses you and others will continue to collectively fail to convince people who either
a) download model data and use multiple colors for each mode (which reveals that Ed choice of grey bands to illustrate “internal variability” with a grey band misleads one into thiniking that spread might be internal variability)
b) Know the that sqrt(x^2+y^2) greater than |x| when |y|≠0.
Are we to be treated to more grey bands that fail to distinguish between the spread due to thhe variability across models and that due to internal variability in the AR5? (Are the time series available on line? I’d be happy to add colored lines for model runs to your graph.)
Thanks Lucia.
The reason for making the examples as I did was to demonstrate that the projections are not outside the range of possibilities projected by CMIP3/5, as some blogs have indicated. I can easily enough add some lines to the plots, like you have, and I will try and get round to doing that.
As for separating the sources of uncertainty – I have done a lot of that – the header image from this blog is from a paper of mine which does exactly what you suggest I think. You can get a copy here: http://www.met.reading.ac.uk/~ed/publications/hawkins_sutton_2010_precip_uncertainty.pdf
Comments welcome. And there will hopefully be a similar figure in AR5. But, I agree that some of the grey spread is model uncertainty, and some is internal variability.
Also, much of the CMIP5 data is available from the Climate Explorer (http://climexp.knmi.nl) if you want to download it. And, I believe all CMIP5 models include volcanic eruptions.
cheers,
Ed.
Lucia – you may also be interested in another post, which showed how variable the variability itself is, even when you remove any changes in forcings, and use the pre-industrial control simulations:
http://www.climate-lab-book.ac.uk/2010/global-mean-temperature-variability/
cheers,
Ed.
ZT–
The paper you cite says “Since the inverse CFD modeling is
ill-posed, this paper has proposed to solve a quasi-reversibility (QR) equation for contaminant transport” and
“The inverse CFD model could identify the contaminant source locations but not very accurate contaminant source strength due to the dispersive property of the QR equation. The results also show that this method works better for convection dominant flows than the flows that convection is not so important”
The reason it works better for convection dominated flows is those are the ones where the diffusive process doesn’t matter much. It’s the diffusive process that has difficulties if you try to go backwards.
Thanks for letting me know the new runs are at the climate explorer. I’ll go have a look. Chad masked the AR4 runs for some comparisons we did. Of course that needs to be done.
I’ve looked at the variability in the variability myself. Some models have huge variability some small. Moreover, it’s also it seems to me if you try examine how variability of “N” year trends varies with N, some models decay nicely while others do not. That said: I think it’s quite possible to show that the variability in some models in inconsistent with earth variability. When doing this, it’s important to remove the variability induced by dramatic swings in applied forcings (e.g. Pinatubo ) as the suggestion that the high variability under smooth seen in a some of the more variable models doesn’t become believable merely because the earth’s temperature do swing in response to a volcanic eruption.